8. 벡터와 행렬
벡터의 Norm
- 원점에서부터의 거리를 의미한다.
- $ L_{1} $ Norm : 각 성분의 변화량의 절댓값
$$ \parallel x \parallel _{1} = \sum_{i=1}^d | x_{i}| $$ - $ L_{2} $ Norm : 피타고라스 정리를 이용한 유클리드 거리를 계산
$$ \parallel x \parallel _{2} = \sqrt{ \sum_{i=1}^d | x_{i}|^2 } $$
Norm의 종류에 따라 기하학적 성질이 달라진다.
서로 다른 Norm을 사용하게 되면 거리의 개념이 달라지기 때문에 원(원점에서부터의 거리)도 기하학적인 모양이 달라진다.
- $ L_{1} $ Norm : Robust 학습, Lasso 회귀
- $ L_{2} $ Norm : 라플라스 근사, Lidge 회귀

두 벡터 사이의 각도
- 제2 코사인 법칙을 이용하여 두 벡터 사이의 각도를 계산할 수 있다.
$$ cos \theta = \frac{ \parallel x \parallel^{2}_{2} + \parallel y \parallel^{2}_{2} - \parallel x-y \parallel^{2}_{2} }{ 2\parallel x \parallel_{2} \parallel y \parallel_{2} } $$
$$ cos \theta = \frac{<x,y>}{ \parallel x \parallel_{2} \parallel y \parallel_{2} } $$
내적
- 내적은 정사영된 벡터의 길이와 관련이 있다.
$ Proj(x) $ 의 길이는 $ \parallel x \parallel cos \theta $이다.

- 내적은 정사영의 길이를 벡터 $ y $의 길이 ( $ \parallel y \parallel $ )만큼 조정한 값이다.
$$ <x, y> = \parallel x \parallel_{2} \parallel y \parallel_{2} cos\theta $$ - 내적은 두 벡터의 유사도를 측정하는데 사용한다.
행렬
- 행렬은 벡터공간에서 사용되는 연산자로 이해할 수 있다.
모든 선형변환은 행렬곱으로 계산할 수 있다. - 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다.
패턴을 추출할 수 도 있고, 데이터를 압축할 수 도 있다.
역행렬
- $ A^{-1} $
- 행렬 $ A $와 역행렬 $ A^{-1} $를 곱하면 단위행렬 $ E $ 가 나온다.
$$ AA^{-1} = A^{-1}A = I $$
- 역행렬은 행과 열의 숫자가 같고, 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다.
- 행과 열의 갯수가 달라 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈 역행렬(Moore-Penrose) $ A^{+} $을 이용한다.

- $ R^{m} $ : m차원 공간, $ R^{n} $ : n차원 공간
- $ n >= m $ 인 경우 : 행의 개수가 열의 개수보다 많아지는 경우
$$ A^{+} = (A^{T}A)^{-1}A^{T} $$
$$ A^{+}A = I $$ - $ n <= m $ 인 경우
$$ A^{+} = A^{T}(AA^{T})^{-1} $$
$$ AA^{+} = I $$
- $ n >= m $ 인 경우 : 행의 개수가 열의 개수보다 많아지는 경우
유사역행렬 응용
▮연립방정식
A는 행의 개수와 열의 개수가 다르기 때문에 유사역행렬을 이용해 해를 구할 수 있다.

▮선형회귀분석
유사역행렬을 이용하면 데이터를 선형모델로 해석하는 선형회귀식을 찾을 수 있다.
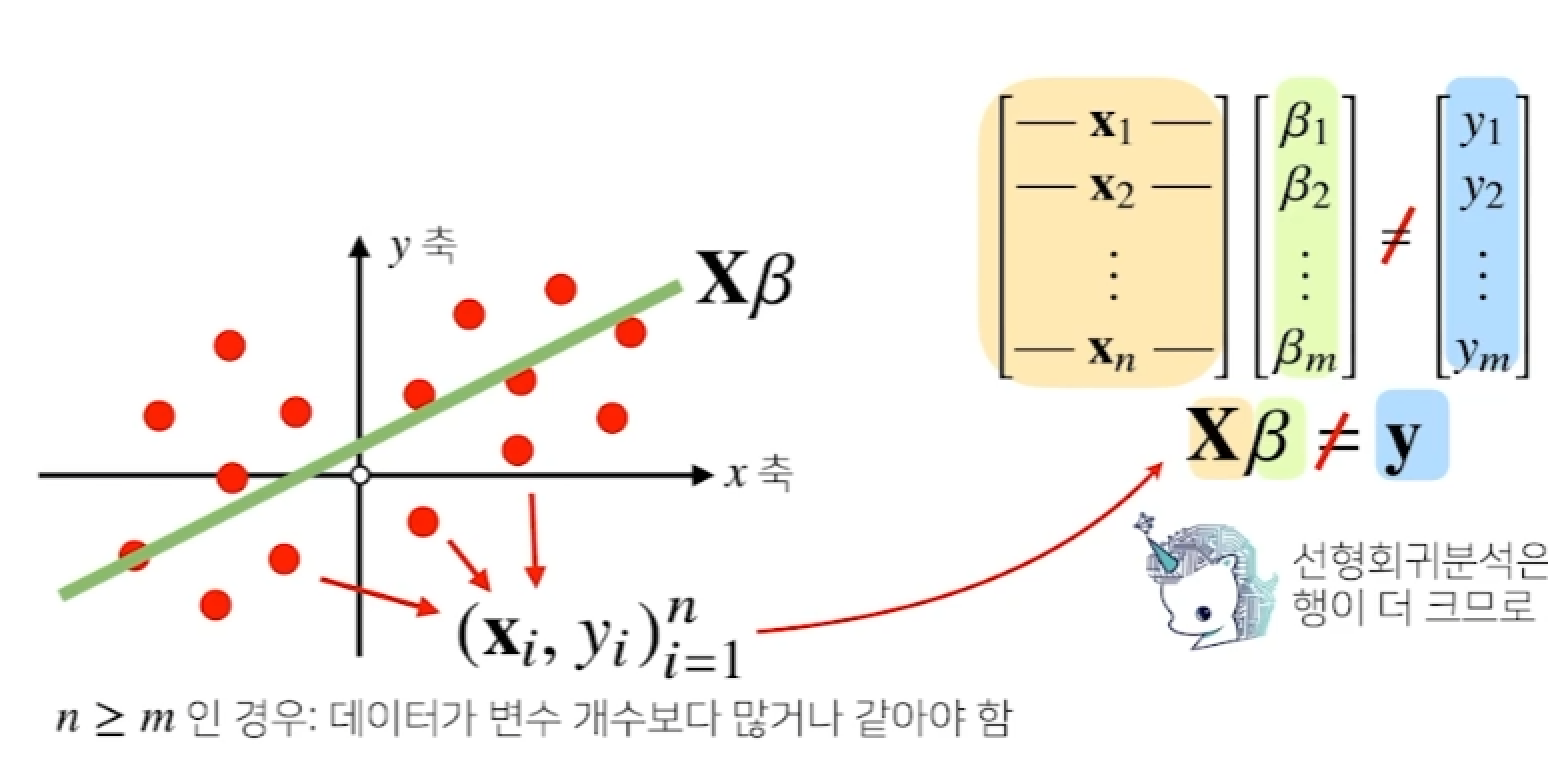
왼쪽 아래 그래프처럼 여러 개의 점을 행렬 $ X $ 를 표현할 수 있다. 이 행렬 $ X $ 에 coefficient 벡터인 $ \beta $ 를 곱해주게 되면 초록색 선으로 표현되게 되는 선형식을 만들 수 있다.
선형회귀분석의 목적은 빨간색 점들을 잘 표현하는 선형모델식을 만들기 위한 $ \beta $ 값을 찾는 것이다.
선형회귀분석은 연립방정식과 달리 행이 더 많기 때문에 방정식을 푸는 것은 불가능하다.
$ {X}\beta = y $ 를 만족하는 $ x $를 찾는 것은 불가능하다.
그렇다면 어떻게 $ \beta $ 값을 찾아야 할까?
데이터의 y값을 예측한 값인 $ \hat{y} $과 실제 $ y $ 값의 차이가 최소화되는 선을 찾았을 때, 적절한 선형모델을 찾았다고 할 수 있다.
즉, $ L_{2} $ Norm을 최소화하는 계수 $ \beta $ 를 찾게되면 선형모델을 이용해서 주어진 데이터를 잘 표현했다고 할 수 있다.

부스트캠프 AI Tech 교육 자료를 참고하였습니다.