[NLP] 3. Basics of Recurrent Neural Network
RNN Basic Structure

RNN은 Sequence 데이터가 입력/출력으로 주어진 상황에서
각 timestep에서 들어오는 입력 벡터 $x_{t}$와 그 전 timestep의 RNN 모듈에서 계산한 hidden state 벡터 $h_{t-1}$을 입력으로 받아 → 현재 timestep에서의 $h_{t}$를 출력으로 내어주는 구조이다.
서로 다른 Timestep에서 들어오는 입력 데이터를 처리할 때, 동일한 parameter를 가진 동일한 모듈을 매 Timestep에서 사용한다.
즉, 상단의 왼쪽 그림같이 동일한 RNN 모듈 A가 매 Timestep 마다 재귀적으로 호출되면서 A 모듈의 출력이 다음 Timestep 에 입력으로 들어가는 형태로 이해할 수 있다.
Calculate the hidden state of RNN

- $x_{t}$ :Timestep t 에서의 입력벡터
- $h_{t-1}$ :이전 Timestep에서의 RNN 모듈에서 계산된 hidden state vector
- $f_{w}$ : W를 parameter로 가지면서 $h_{t-1}$와 $x_{t}$를 입력으로 받는 RNN 함수
- $h_{t}$ : 정보들을 잘 조합해서 계산된 현재 Timestep $t$에서의 hidden state vector
- $y_{t}$
- 최종 예측값을 계산해야 하는 경우에는 $h_{t}$를 바탕으로 $y_{t}$를 계산할 수 있다.
- 예측값을 나타내는 output $y_{t}$는 매 Timestep 마다 계산해야 할 수도 있고(각 단어 별 품사 예측)
아니면 마지막 Timestep 에만 계산 해야하는 경우도 있다.(문장의 긍정 부정 분류)

timestep t에서 들어온 단어의 임베딩 벡터($x_{t}$)가 3차원 벡터이고, $h_{t-1}$은 2차원이라고 가정하자.
hidden state vector의 차원 수는 RNN에서 정의해야 하는 hyper parameter이다.

$x_{t}$와 $h_{t-1}$으로 구성된 5개의 입력 node를 통해서 $h_{t}$를 계산한다.
$h_{t}$의 dimension은 $h_{t-1}$과 동일한 형태의 dimension 을 공유해야 하기 때문에 dimension은 2여야 한다.

fully connected layer의 어떤 linear transformation matrix를 W 라고 정의하면 아래와 같이 행렬곱을 나타낼 수 있다.

5차원 간의 내적은 첫번째 부분에 있는 2차원 vector와 입력으로 주어진 $h_{t-1}$ 그리고 두번째 부분에 있는 3차원 vector 와 두번째 입력 부분으로 주어지는 $x_{t}$와 각각 내적을 해준 후 그 다음에 2개의 내적값을 더해주면 $h_{t}$의 첫번째 node 의 값을 구할 수 있다.

- $w_{hh}$ : $h_{t-1}$를 $h_{t}$로 변환해주는 행렬
- $w_{xh}$ : $x_{t}$를 $h_{t}$로 변환해주는 행렬
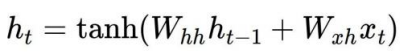
이렇게 구해진 $h_{t}$를 비선형변환 함수인 tanh를 통과시켜줌으로써 최종적인 RNN 모듈의 현재 timestep의 hidden state vector $h_{t}$를 계산할 수 있다.

현재 Timestep t 에서 task의 예측값이 필요한 경우에는$h_{t}$를 입력으로 하는 추가적인 layer인 output layer를 만들고
그 output layer에 linear transformation matrix인 $W_{hy}$를 곱함으로써 최종 output 인 $y_{t}$
Types of RNNs

- one to many
- Image에 대한 설명글을 생성하기 위해서 그에 필요한 단어를 각 timestep 별로 순차적으로 생성하는 Task
- RNN 구조는 timestep 마다 입력이 주어지는 데, 추가적으로 넣어줄 입력이 딱히 없는 경우에는 같은 사이즈의 vector나 행렬 혹은 tensor가 들어가되, 모두 값이 0으로 채워진 형태의 입력을 준다.
- many to one
- Sentiment Classifcation
- ‘I love movie’ 라는 입력 문장이 주어지면 각각의 단어를 word embedding 형태로 입력으로 각 timestep 에서 받아서 이 RNN 모듈이 입력으로 주어지는 데이터를 잘 처리한 후 마지막 timestep 에서 나온 $h_{t}$를 가지고 최종적인 output layer 를 적용함으로써 긍정 혹은 부정에 해당하는 값을 예측한다.
- many to many
- Machine translation
- PoS tagging
Character-level Language Model
- Language Model Task 는 기본적으로 주어진 문자열이나 단어들의 순서를 바탕으로 그 다음단어가 무엇인지를 맞추는 Task이다.
Language Modeling 은 word level 혹은 character level 에서 모두 다 수행 할 수 있다. - 여기서는 character level , 학습데이터로서 단 하나의 단어인 “hello” 라는 단어만이 주어져 있다고 가정하자.
- Example training sequence: “hello”
- Vocabulary: [h, e, l, o]
주어진 학습 데이터로부터 찾을 수 있는 unique한 character를 중복 없이 사전을 구축한다.
그 후 각각의 character 는 총 사전의 갯수 만큼의 dimension을 가지는 one-hot vector 로 나타낸다. (h : [1 0 0 0])

character를 가지고 language model을 수행하는 경우, 주어진 character의 sequence 가 h, e, l, l 의 순으로 주어지게 되면
첫 번째 timestep input인 h가 주어졌을 때 바로 h 다음에 나올 character인 e를 예측해야 하고
두번째 timestep에서 h 와 e 까지 주어지게 되면 그 다음에 나타나는 character 인 l 을 예측하는 task를 RNN 구조를 통해 다룰 수 있다.
첫번째 timestep에서 주어지는 [1 0 0 0] 이라는 $x_{t}$와 첫번째 timestep에서는 $h_{0}$ hidden state vector 가 입력으로 필요하게 되는데 이 경우에는 그 전의 timestep 에서 RNN 모듈이 실행되지 않았기 때문에 default 로 모두 0 인 vector 를 RNN 의 입력으로 주게 된다.

character level의 language modeling 에서 각 timestep 마다 다음에 나올 character 를 예측해야되는 task 이므로 이는 many-to-many task이다.
즉 이 output vector 를 계산하기 위해서 해당 timestep에서 구해진 $h_{t}$를 output layer에 적용해서 최종 output 을 얻어낸다.

output layer에서 정의된 선형변환의 parameter $W_{hy}$를 $h_{t}$와 곱하고 그 다음에 bias term 까지 같이 고려를 해서 output vector 를 얻어낸다.
이 값이 logit 이라고 표현된 이유는 사전에서 정의된 4개의 character 중 다음에 나올 character 를 예측하는 task이기 때문에 output layer의 node수는 사전의 크기와 동일한 4개의 dimension 으로 이루어진 output vector가 나오기 때문이다.

softmax의 입력으로 들어가는 logit 값으로서의 output vector가 제일 큰 값을 가질 때, 해당 확률값이 가장 큰 값으로 나오게 된다.
위 그림에서는 'o'가 제일 큰 확률이 나왔지만 ground-truth character는 e 이기 때문에 여기에서 나오는 2번째 확률값을 최대한 높이도록 softmax loss를 적용해서 학습하게 된다.

Inference 시에는 첫번째 character 만을 입력으로 주고 그 다음엔 그 해당 timestep에서의 예측값을 그 다음 timestep 의 입력으로 재사용해서 또 다음 character 를 예측하는 과정을 거쳐 무한한 길이의 character sequence 를 자유롭게 생성할 수 있다.
Backpropagation through time (BPTT)
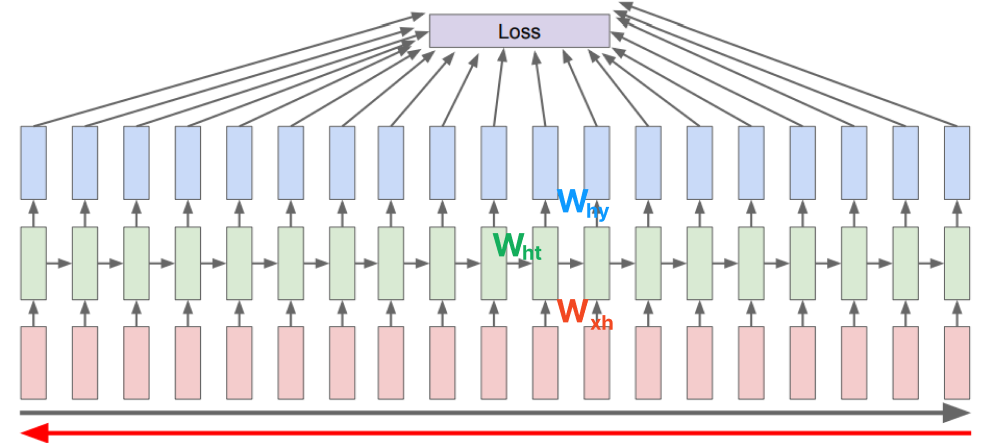
$W_{xh}$, $W_{ht}$, $W_{hy}$는 backpropagation에 의해 학습이 진행된다.

나오는 output 을 모두 다 계산하고 loss를 적용한 후 backpropagation 과정을 수행해야 하는데 현실적으로 이 길이가 굉장히 길어지면 한꺼번에 처리할 수 있는 정보나 데이터의 양이 한정된 GPU resource 내에서의 memory에 모두 다 담기지 못할 수 있다.
그래서 군데군데 잘라서 그에 해당하는 제한된 길이의 sequence 만으로 학습을 진행하는 truncation 방식을 채택한다.
Searching for Interpretable Cells
RNN 에서 필요로 하는 정보를 저장하는 공간은 매 timestep마다 업데이트를 수행하는 $h_{t}$라고 할 수 있다.
(ex. 공백을 2번 혹은 4번을 생성해야한다는 정보)

hidden state vector의 차원이 3차원이라고 가정한다면 그 필요한 정보가 3개의 숫자중 어디에 저장이 되어있는가를 역추적하는 식으로 분석을 수행할 수 있다.
특정한 hidden state vector의 dimension 을 고정해놓고 그 해당 dimension 의 값이 어떻게 변하는가를 값이 (-)로 값이 클 때에는 파란색으로, 그 값이 (+)로 값이 커질때는 빨간색으로 나타낸 시각화의 예시는 아래와 같다.

“ 가 열리고 닫히는 동안 항상 값이 (-)로 큰 값을 유지가 됐다가 “ 가 닫히고 나서는 다시 빨간색 값으로 유지가 되는 것을 볼 수 있다.
→ RNN 내에서 hidden state vector 의 특정 dimension이 하는 역할을 알 수 있다.
→ “ 가 현재 열렸다 혹은 닫혔다에 대한 상태를 기억하고 있는 역할을 하는 것!
Vanishing/Exploding Gradient problem in RNN
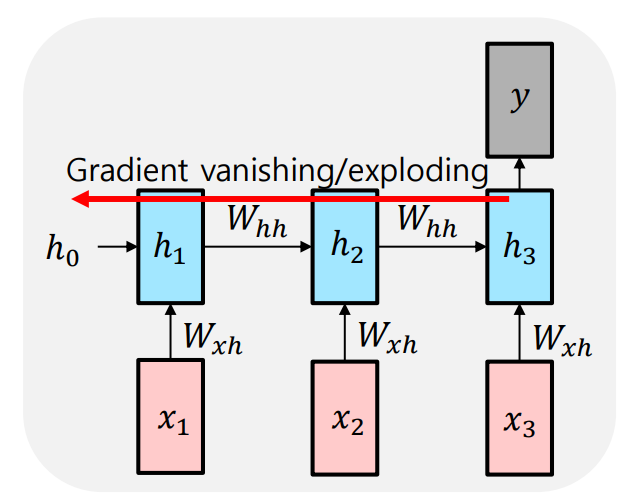
가 반복적으로 반영이 된다는 사실때문에 등비수열과 같은 같은 수가 계속해서 곱해지게 된다.
backpropagation에서도 마찬가지로 같은 숫자가 계속적으로 곱해짐으로써 graidient가 기하급수적으로 커지거나 혹은 공비가 1보다 작을 때는 기하급수적으로 값이 작아지게 되는 문제점이 발생한다.
부스트캠프 AI Tech 교육 자료를 참고하였습니다.