[LM metric] Perplexity
- -
Evaluate Language Models
언어 모델의 평가 방식은 크게 2가지로 구분할 수 있다.
- 외부적 평가(Extrinsic): 언어모델을 특정 태스크에 적용해서 loss/accuracy를 사용하여 확인하는 방법
- 내부적 평가(Intrinsic): 태스크에 적용하지 않고 언어모델의 자체적인 역량을 평가하는 방법
외부적 평가방법에 비해 정확하지는 않겠지만 모델별 비교에 적합
Perplexity
Perplexity는 내부적 평가 방식에 해당한다.
Perplexity is the inverse probability of the test set, normalized by the number of words
Perplexity는 단어의 수로 정규화된 테스트 데이터셋에 대한 확률의 역수이다.
: 테스트 문장에 대해서 언어 모델을 이용하여 확률(likelihood)를 구하고 문장의 확률을 길이에 대해서 normalization(기하평균)
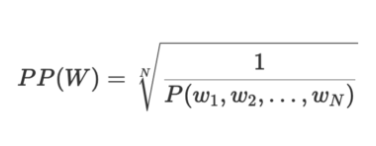
주사위 확률을 가지고 간단하게 Perplexity를 해석해본다면,
가정: 1부터 6까지 이루어진 주사위의 출현 확률이 같다
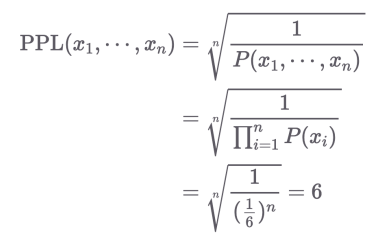
주사위의 PPL: 매 time-step마다 가능한 경우의 수가 6가지
→ PPL이 낮을 수록 확률 분포가 sharp
→ PPL이 높을 수록 확률 분포가 flat
즉, 언어 모델에서 본다면 매 time-step마다 평균적으로 헷갈리고 있는 단어의 수라고 볼 수 있다.
probability of the test set
좋은 언어모델은 적합한 문장에는 높은 확률을 부여하고 부적합한 문장에는 낮은 확률을 부여한다.
(실제 사용하는 언어의 분포를 가장 잘 근사하는 모델)
즉, test set에 가장 높은 확률을 부여하는 모델이 좋은 모델임을 의미한다.
Normalising
문장은 길이도 가지각색이고 단어의 수도 가지각색이다. 문장의 길이가 길수록 불확실성이 커질 수 있으므로 전체 단어 수로 test set의 확률을 정규화한다. 이를 통해 단어별 측정이 가능하다.
unigram 모델을 예로 들어보겠다.
unigram 모델의 문장 확률은 다음과 같다.
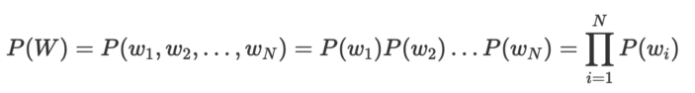
해당 확률을 정규화하려면 로그를 취해 덧셈 합으로 바꿔준 뒤
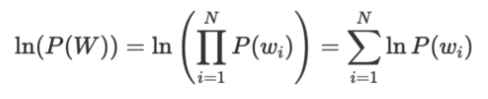
N으로 나누어 단어 당 로그 확률을 구할 수 있다.
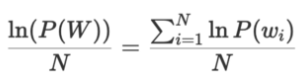
그 다음 지수화를 하여 로그를 제거하면 1/N 루트를 취하여 정규화값을 얻을 수 있다.
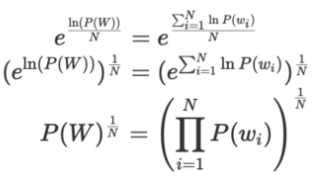
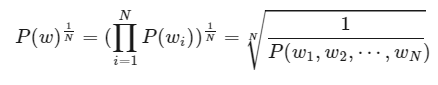
Note )
- 확률의 역수이기 때문에 perplexity 값이 작을 수록 좋은 모델이다.
- <SOS> , <EOS> 토큰도 단어의 개수에 포함한다.
Perplexity as the exponential of the cross-entropy
정보이론에서 엔트로피는 어떤 정보의 불확실성을 나타낸다.
: 자주 발생하는 일(일어날 확률이 높은 일)은 낮은 정보량
: 드물게 발생하는 일(일어날 확률이 낮은 일)은 높은 정보량
→ 정보량 : 확률이 0에 가까워질수록 높은 정보량
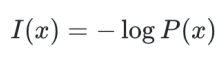
언어 모델 관점에서 바라본다면 흔히 나올 수 없는 문장일수록 더 높은 정보량을 갖고 있다고 볼 수 있지 않을까?
따라서 Perplexity 는 exponential of the cross-entropy를 이용해도 계산할 수 있다.
Cross entropy는 다음과 같다.
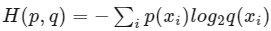
단어 배열 W의 크기가 크다면(문장의 길이가 길며 N이 클 때) Shannon-McMilan-Breiman theorem에 따라 cross-entropy를 다음과 같이 근사시킬 수 있다.

이를 언어 모델 P에 적용해보면 다음과 같이 distribution 간의 cross entropy를 정의할 수 있다.
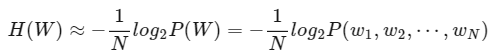
이를 활용하여 Perplexity는 cross-entropy의 exponential로 재정의할 수 있다.
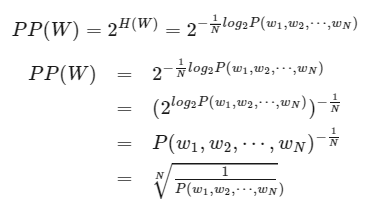
즉, perplexity는 test set에 대한 loss로 계산할 수 있다
# Masked Language Model의 Perplexity
BERT 스타일의 encoder 모델의 경우 masked token에 대한 nll loss의 exponential로 계산할 수 있다.
from transformers import AutoModelForMaskedLM, AutoTokenizer
import torch
import numpy as np
model_name = 'cointegrated/rubert-tiny'
model = AutoModelForMaskedLM.from_pretrained(model_name)
tokenizer = AutoTokenizer.from_pretrained(model_name)
def score(model, tokenizer, sentence):
tensor_input = tokenizer.encode(sentence, return_tensors='pt')
repeat_input = tensor_input.repeat(tensor_input.size(-1)-2, 1)
mask = torch.ones(tensor_input.size(-1) - 1).diag(1)[:-2]
masked_input = repeat_input.masked_fill(mask == 1, tokenizer.mask_token_id)
labels = repeat_input.masked_fill( masked_input != tokenizer.mask_token_id, -100)
with torch.inference_mode():
loss = model(masked_input, labels=labels).loss
return np.exp(loss.item())
print(score(sentence='London is the capital of Great Britain.', model=model, tokenizer=tokenizer))
# 4.541251105675365
print(score(sentence='London is the capital of South America.', model=model, tokenizer=tokenizer))
# 6.162017238332462
# Autoregressive Language Model의 Perplexity
GPT 스타일의 decoder 모델에서는 다음 token에 대한 nll loss의 exponential로 계산할 수 있다.
( hugging face docs : https://huggingface.co/docs/transformers/perplexity )
from transformers import GPT2LMHeadModel, GPT2TokenizerFast
device = "cuda"
model_id = "gpt2-large"
model = GPT2LMHeadModel.from_pretrained(model_id).to(device)
tokenizer = GPT2TokenizerFast.from_pretrained(model_id)WikiText-2 dataset를 갖고 Perplexity를 계산해본다.
데이터셋이 크지 않기 때문에 전체 데이터 세트를 한번에 인코딩한다.
from datasets import load_dataset
test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encodings = tokenizer("\n\n".join(test["text"]), return_tensors="pt")
# {'input_ids': tensor([[ 628, 796, 5199, ..., 220, 628, 198]]), 'attention_mask': tensor([[1, 1, 1, ..., 1, 1, 1]])}
huggingface에서는 sliding window를 적용하였으며 ppl을 계산한다.
import torch
from tqdm import tqdm
max_length = model.config.n_positions
stride = 512
nlls = []
for i in tqdm(range(0, encodings.input_ids.size(1), stride)):
begin_loc = max(i + stride - max_length, 0)
end_loc = min(i + stride, encodings.input_ids.size(1))
trg_len = end_loc - i # may be different from stride on last loop
input_ids = encodings.input_ids[:, begin_loc:end_loc].to(device)
target_ids = input_ids.clone()
target_ids[:, :-trg_len] = -100
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
neg_log_likelihood = outputs[0] * trg_len
nlls.append(neg_log_likelihood)
ppl = torch.exp(torch.stack(nlls).sum() / end_loc)슬라이딩 윈도우 방식을 사용하면 iteration 과정에서 모델에 전달하는 토큰이 겹친다.
(0 512) (0 1024) (512 1536) ...
마지막 token에 대한 loss만 계산하기 위해 tar_len까지는 모두 -100으로 두어 ignore한다.
최종적으로 계산한 nll loss의 평균을 사용하여 ppl을 계산한다.
stride가 작을 수록 모델이 prediction마다 더 많은 context을 갖기 때문에, perplexity가 일반적으로 더 좋게 나온다.
stride = 1024일 때 PPL 은 19.64(GPT2 논문에서는 19.93),
stride = 512일 때는 PPL은 16.53이 나온다.
Reference )
https://soundprovider.tistory.com/entry/LM-Perplexity-%EA%B0%9C%EB%85%90?category=1126750
https://towardsdatascience.com/perplexity-in-language-models-87a196019a94
'딥러닝 > 자연어 처리' 카테고리의 다른 글
| How to generate text: decoding methods (0) | 2022.06.15 |
|---|---|
| [LM metric] BLEU(Bilingual Evaluation Understudy) (0) | 2022.06.08 |
| GPT & GPT2 (0) | 2022.06.04 |
| [CS244n] Transformers & Pretraining (0) | 2022.05.31 |
| [CS244n] Self-Attention & Transformer (0) | 2022.05.29 |