14. CNN

MLP의 경우 각 뉴런들이 선형모델과 활성화함수로 모두 연결된 fully connected 구조이다.

아래 그림과 같이 각 성분 $h_{i}$에 대응하는 가중치 행 ${W}_{i}$가 필요하기 때문에 학습시켜야하는 parameter의 수가 커지게 된다.

 

$$ h_{i} = \sigma ( \sum_{j=1}^p W_{ij}x_{j} ) $$

 

 

Convolution 연산

Convolution은 커널이라는 고정된 가중치 행렬을 사용한다.

($i$에 따른 가중치 행이 따로 있는 것이 아니라 모든 $i$에 대해 적용되는 커널이 같다.)

$$ h_{i} = \sigma ( \sum_{j=1}^k V_{j}x_{i+j-1} ) $$

• 모든 $i$에 대해 적용되는 커널은 같기 때문에 parameter 사이즈를 많이 줄일 수 있다.
• 다양한 종류의 커널에 따라 경계선, 노이즈 제거 등 다양한 처리가 가능하여 영상처리에서 많이 사용한다.
• Convolution 연산은 다양한 차원에 적용이 가능하다.
  • 1D-conv: 음성, 텍스트 등
  • 2D-conv: 흑백 이미지
  • 3D-conv: 컬러 이미지 

 

2차원 Convolution 연산

$$ [f*g](i,j) =  \sum_{p,q}^ f(p,q)g(i+p,j+q)  $$

• $f(p,q)$는 커널, $p,q$는 컨볼루션의 위치
• $g(i+p,j+p)$는 입력, $i, j$는 입력좌표

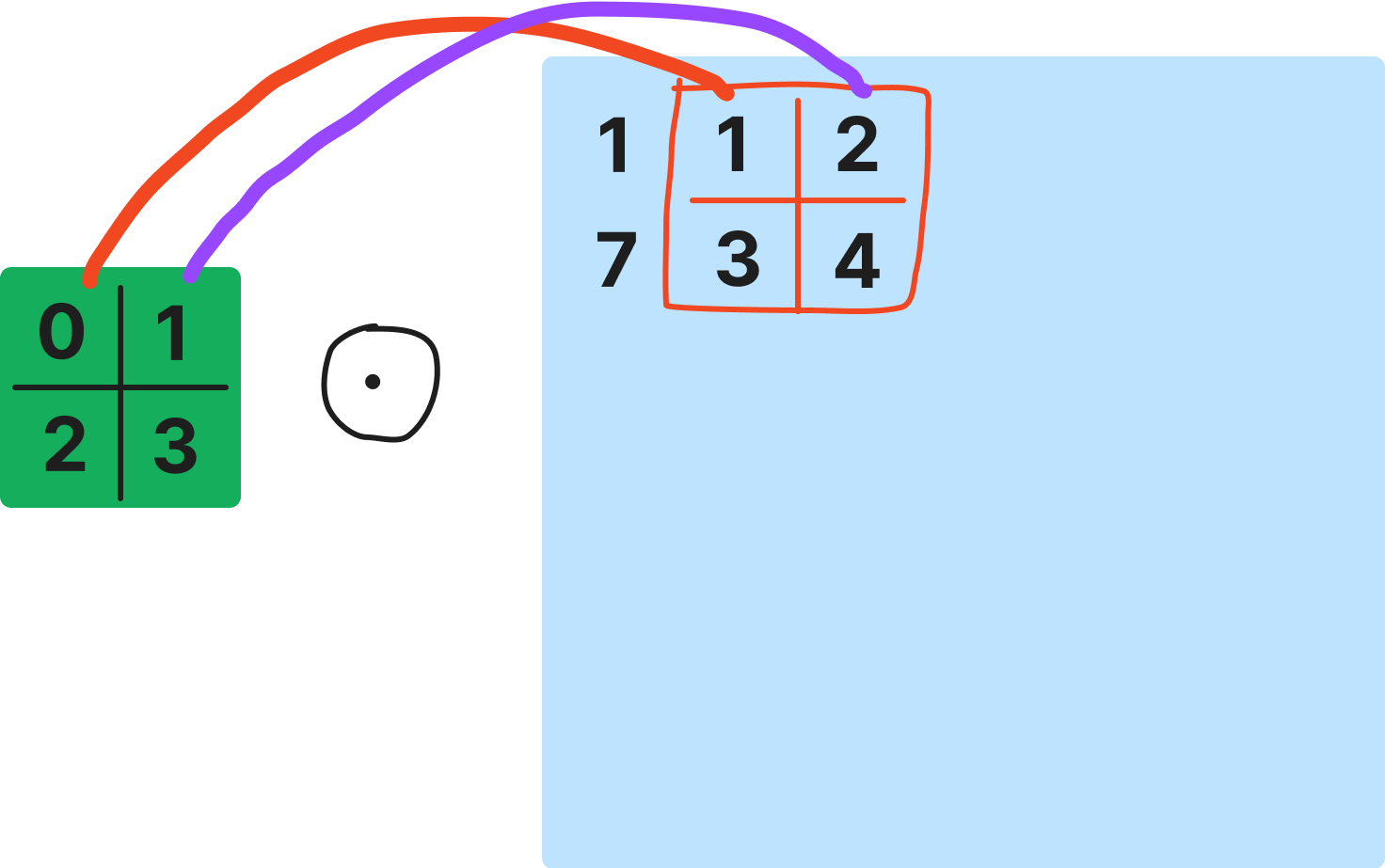
행렬 연산이 아니라 각 위치에 따른 Element Wise Multiplication 연산을 진행한다.

 

• 입력 크기를 $(H, W)$, 커널 크기를 $(K_{H}, K_{W})$, 출력 크기를 ${O_{H},O_{W})$라고 한다면 출력 크기는 아래와 같이 계산할 수 있다.

$$ O_{H} = H - K_{H} + 1 $$

$$ O_{W} = H - K_{W} + 1 $$

 

3차원 Convolution 연산

• 3차원인 경우, 2차원 Convolution을 N번(채널수만큼) 적용한다고 볼 수 있다.

 

Convolution 연산의 역전파

Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 Backpropagation을 계산할 때도 convolution 연산이나온다.

Convolution 연산도 선형변환이기 때문에 MLP의 Backpropagation 계산 방법과 동일하다.

 

업데이트 하고자 하는 파라미터를 커널의 $W_{1}$라고 하자.

 $W_{1}$는 $O_{1}$에서 $x_{1}$과 연결되어 있고 $O_{2}$에서는 $x_{2}$과 연결되어 있고 $O_{3}$에서 $x_{3}$과 연결되어 있다.

따라서 손실함수에 대한 $W_{1}$의 편미분 값은 아래 식과 같이 표현할 수 있다.

$$ \frac{\partial L}{\partial w_{1}} =  \delta_{1}x_{1} + \delta_{2}x_{2} + \delta_{3}x_{3} $$

결국 Backpropagation을 할 때 convolution 연산이 이루어짐을 알 수 있다.

 

 

---

부스트캠프 AI Tech 교육 자료를 참고하였습니다.