[NLP] 5. Seq2Seq with attention
- -
Seq2Seq2 model
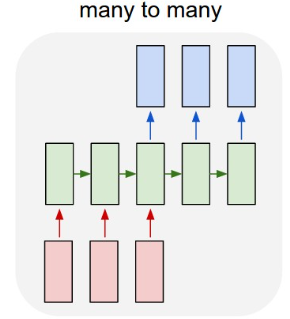
Seq2Seq 모델은 RNN의 구조 중 입력과 출력이 모두 시퀀스의 형태인 many-to-many 형태에 해당한다.
입력 시퀀스를 모두 읽은 후 출력 시퀀스를 예측한다.

- 입력문장을 읽어들이는 RNN 모델을 Encoder, 출력문장을 단어 하나하나씩 생성하는 RNN 모델을 Decoder 라고 부른다.
- Encoder 부분과 Decoder 부분은 서로 share하지 않는 parameter 로 이루어진 RNN 모듈이다.
- RNN계열 모델로 LSTM을 사용하였다.
Seq2Seq model에서 Encoder의 마지막 timestep의 hidden state vector는 바로 Decoder의 첫번째 timestep의 입력($h_{0}$)으로 주어진다.
이 hidden state vector는 Encoder에서 수집한 정보들을 잘 담아두고 있다가 이 정보를 바탕으로 Decoder가 순차적으로 단어를 예측하게 된다.

가장 처음에 <SoS>(start of sentence)토큰을 넣어줌으로써 실질적으로 생성되는 첫번째 단어부터 예측을 수행하게 된다.
문장이 끝나는 시점을 언제까지 단어를 생성할지에 대해서는 <EoS>(end of sentence)토큰이 나올 때까지 Decoder RNN 을 구동하고 이 토큰이 실제로 생성되면 여기까지가 최종적인 출력으로 더이상은 단어를 생성하지않는다.
Seq2Seq2 model with Attention
RNN기반의 seq2seq model 구조는 단어를 순차적으로 읽어들이고 거기서 필요한 정보를 매 timestep마다 축적해가면서 hidden state vector를 생성하는 과정을 따르는데
RNN구조 특성상 hidden state vector의 dimension이 정해져있기 때문에 입력 문장의 길이가 짧은 문장이든 긴 문장이든 Encoder의 마지막 timestep에 있는 hidden state vector에 앞서 나왔던 많은 정보들을 다 담아야한다는 문제점이 있다.
LSTM에서 Long-term dependencies 를 해결했다고 하더라도 마지막 timestep을 기준으로 할 때, 훨씬 이전에 나타났던 단어에 대한 정보는 LSTM 구조를 지나면서 점차 변질되거나 소실될 수 있다.
Attention 모듈의 기본적인 아이디어
Encoder 의 마지막 timestep에서 나오는 hidden state vector 하나에만 의존하는 것이 아니라
입력 문장에서 주어졌던 각각의 단어들을 순차적으로 Encoding하는 과정에서 나오는 Encoder hidden state vector들을 전체적으로 Decoder에 제공해주고
Decoder에서는 각 timestep에서 단어를 생성할 때 그때그때 필요한 Encoder hidden state vector를 선별적으로 가져가서 예측에 도움을 주는 형태로 활용한다.
Attention 모듈의 동작 과정

hidden state vector가 4개의 dimension으로 구성되어 있다고 가정하자.
그냥 seq2seq model처럼 마지막 timestep의 Encoder hidden state vector가 Decoder의 $h_{0}$로 입력으로 들어간다.
그리고 START 토큰으로서 주어지는 토큰의 word embedding vector가 입력으로 주어진다.
이 둘을 입력으로 받아서 Decoder의 hidden state vector $h^{d}_{1}$를 만들어 주게 된다.

이렇게 계산된 Decoder의 첫번째 timestep의 hidden state vector($h^{d}_{1}$)를 가지고 다음 단어의 예측을 수행하는데 사용할뿐만 아니라
이 벡터를 통해 Encoder에서 주어진 4개의 hidden state vector 중 현재 어떤 hidden state vector를 필요로 하는지를 선정하는 역할을 수행한다.
→ $h^{d}_{1}$가 Encoder hidden state vector 각각과 내적의 연산을 수행

내적값이 7 1 -1 -2 라고 가정하면 이 값은 Decoder hidden state vector와 각 Encoder hidden state vector간의 내적에 기반한 유사도라고 볼 수 있다.
이 값들을 각각의 Encoder hidden state vector에 대응하는 확률값을 계산해줄 수 있는 입력벡터 혹은 logit 벡터라고 보고 softmax 를 통과시키면 0.85 0.08 0.04 0.03의 확률값으로 볼 수 있다.

0.85 0.08 0.04 0.03 값은 Encoder hidden state vector에 부여된 가중치로 사용된다.
즉, 4개의 Encoder hidden state vector에 대해서 0.85 0.08 0.04 0.03 가중치 세트를 적용해서 가중 평균으로서 나오는 하나의 Encoding vector 를 구한다. → context vector
즉, 해당 시점에 필요로 하는 정보는 첫번째 timestep의 Encoder hidden state vector를 85% 필요로 하고 있고 두번째는 8% 세번째는 4% 네번째는 3%의 정보를 필요로 하고 있음을 의미한다.
attention module은 위 그림의 큰 초록색 부분으로 볼 수 있다.
Decoder hidden state vector 하나와 Encoder hidden state vector 세트가 attention module의 입력으로 들어간다.
attention module의 출력으로 나오는 것은 Encoder hidden state vector의 가중 평균된 한개의 vector이다.

만들어진 context vector는 앞서 계산한 Decoder hidden state vector와 context vector 함께 concat이 되어 output layer 의 입력으로 들어가게 되고 그로부터 다음에 나올 단어를 예측한다.

두 번째 timestep에서는 해당 timestep에서 들어오는 입력 단어(the)와 첫번째 timestep 에서 넘어온 Decoder hidden state vector인 $h^{d}_{1}$를 입력으로 받아 RNN 을 통과해 $h^{d}_{2}$를 만든다.
그리고 동일한 attention module을 다시한번 사용하되, $h^{d}_{2}$를 가지고 Encoder hidden state들과 내적을 계산한다.
이렇게 Attention module을 이용하여 timestep마다 서로 다른 가중치를 Encoder hidden state vector에 적용해서 나오는 가중평균된 vector를 그때그때마다 output layer 에 직접적인 입력의 일부로서 사용해 해당 timestep에서의 예측에 좀 더 정확도를 올릴 수 있다.
Decoder RNN의 hidden state vector의 역할은 2가지로 볼 수 있다.
1. 해당 timestep 에서의 output 단어(다음에 등장해야 하는 단어)를 예측하는 output layer 에 입력으로 사용
2. 입력 sequence에서 주어지는 각 word 별 Encoding vector 중 어떤 단어 vector를 중점적으로 가져와야 할지 attention 가중치를 결정

왼쪽은 Teacher forcing 방식은 Decoder에서 각 timestep에서의 예측을 잘못한 경우( 예를 들어 토큰 이후 첫번째 단어로 'the' 가 나와야 하는데 'a' 라는 단어를 예측을 하는 경우 ) 전단계에서 예측을 잘못했다 하더라도 다음 timestep 에서는 ground-truth 단어를 입력으로 넣어주는 것이다.
반면에 오른쪽은 실제 예측값이 맞는 값이든 아니든 그 단어를 실제로 다음 timestep에 입력으로 넣어주는 이러한 방식이다.
Teacher Forcing 을 쓰는 경우에는 실제 ground-truth 를 넣어주기 때문에 학습이 좀 더 빠르고 용이하게 학습이 진행이 될 수 있는 장점이 있긴 하지만 실제로 모델을 사용할때의 상황과는 괴리를 갖는다.
이 둘을 적절히 병합한 그러한 학습방식도 존재한다.
처음에는 Teacher Forcing만으로 모든 배치를 구성해서 학습을 진행하다가 모델이 어느정도 예측이 정확해지면 학습의 후반부에는 Teacher Forcing을 사용하지 않고 실제로 예측한 값을 다음 timestep의 입력으로 주는 식으로 실제 이 모델이 사용되는 test-time 에서의 상황에 좀 더 부합하도록 학습을 점점 변화시켜주는 방식이다.
Different Attention Mechanisms
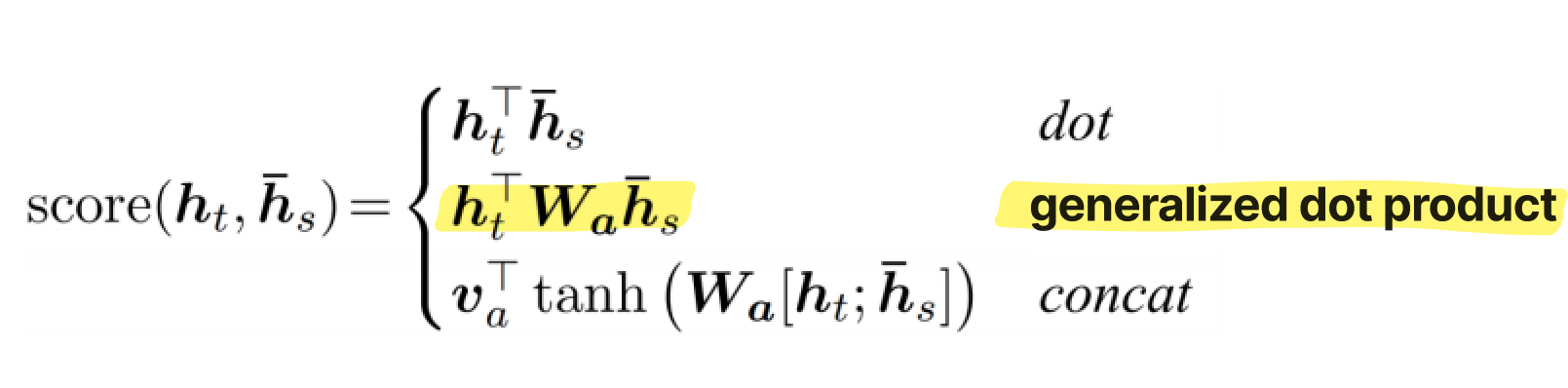
$h_{t}$가 Decoder에서 주어지는 hidden state vector이고, $\bar{h}_{s} $가 Encoder 단에서의 각 word 별 hidden state vector라고 할 때,
이 둘간의 유사도를 구하기 위해서(score function) 내적을 할 수도 있지만, 내적을 조금 더 확장한 형태의 generalized dot product를 할 수도 있다.
generalized dot product
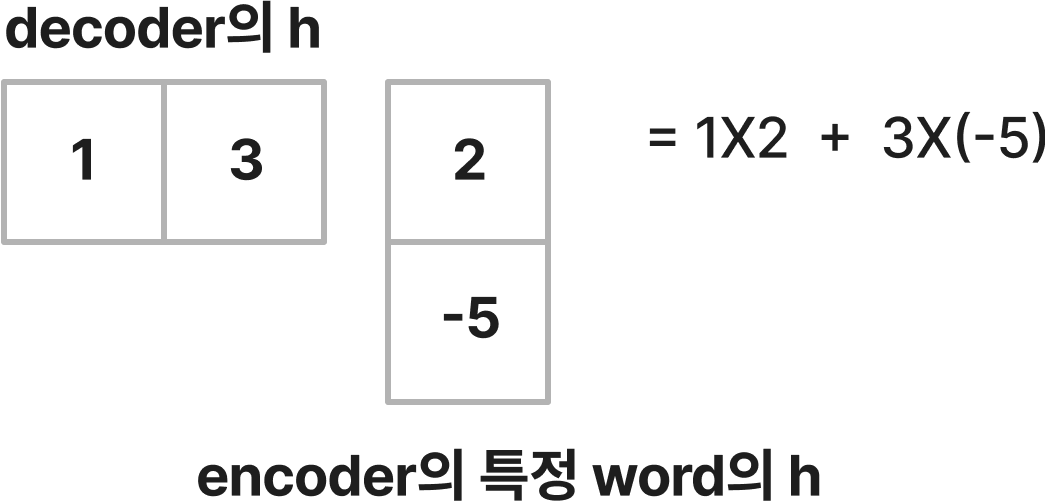
decoder의 hidden state 벡터와 encoder의 특정 word의 hidden state 벡터의 내적을 계산하는 방법은 위 그림과 같다.여기에 아래처럼 항등행렬 I를 곱해주어도 같은 값이 나온다.

그렇다면 항등행렬의 값을 아래 그림처럼 1에서 4로 바꿔주게 된다면 첫번째 dimension의 곱에는 가중치 1, 두번째 dimension의 곱에는 가중치 4가 부여됨을 알 수 있다.

그렇다면 이번에는 위에서 추가로 0인 부분을 각각 아래와 같이 7과 8로 바꿔보았다.

그러면 기존 항에 두개의 항이 추가됨을 알 수 있다.

이때 (-8)x3x2에서 3과 2는 첫번째 벡터의 두번째 dim, 두번째 벡터의 첫번째 dim을 곱한 값이다.
7x1x-5에서 1과 -5는 첫번째 벡터의 첫번째 dim, 두번째 벡터의 두번째 dim을 곱한 값이다.
그리고 각 항의 (-8)과 7이 각각 서로 다른 dim을 곱해서 만들어지는 결과값에 곱해지는 가중치임을 알 수 있다.
즉, 가운데 행렬을 a, b, c, d라는 학습가능한 파라미터로 두게 되면 a,b,c,d는 주어진 벡터에서 모든 dim들간의 곱해진 값들에 각각 부여되는 가중치라고 볼 수 있다.
원래 간단한 내적을 통해 유사도를 구하는 방식을, 가운데 학습가능한 행렬을 추가함으로서 간단한 내적 연산을 확장한 형태로 attention score값을 구할 수 있다.
→ 일반화된 dot product라는 형태로 가운데에 있는 $W_{a}$ attention module 에서의 유사도를 결정해주는 학습가능한 parameter 의 형태로 모델이 구성될 수 있다.
concat 기반

decoder의 hidden state 벡터와 encoder의 특정 word의 hidden state 벡터가 입력으로 주어졌을 때, 두 벡터간의 유사도를 구하는(최종적으로 scalar값이 나오도록하는) multi-layer perceptron이라는 추가적인 학습가능한 neural net을 만드는 방법이다.

decoder의 hidden state 벡터와 encoder의 특정 word의 hidden state 벡터를 concat해서 fully-connected layer를 두는 모델을 구성할 수 있다.

또는 layer를 더 쌓는 형태로 구성할 수도 있다.
이렇게 유사도를 구해야하는 두 벡터가 concat이 되어서 유사도를 구하는 multi-layer neural net에 입력으로 들어가기 때문에 concat 기반의 attention 방식이라고 부른다.
Decoder의 hidden state vector $h_{t}$와 Encoder에서의 특정 word 의 hidden state vector $\bar{h}_{s} $둘을 concat(;) 한 뒤 첫번째 layer(수식에서는 $W_{a}$, 그림에서는 $W_{1}$)의 선형변환을 거치고 그 다음에는 tanh를 non-linear unit 으로 적용해주고 두번째 layer에서는 선형변환에 해당하는 $v^{T}_{a}$를 거친다.(그림에서는 $W_{2}$)
$v^{T}_{a}$가 행렬의 형태가 아니라 vector의 형태로 쓰인 이유는 첫번째 layer 를 거쳐서 나온 값이 vector이기 때문에 최종 결과물인 scalar 값을 만들기위해 vector의 형태가 되어야한다.

최적화가 필요한 parameter 들은 어떻게 최적화가 되는가?
위 그림의 (노랑색 형광펜으로 칠한 부분)원래는 학습 가능한 파라미터가 포함되지 않았던 단순한 내적값의 부분이
학습을 필요로하는 파라미터가 포함된 모듈로 바뀌었기 때문에 backpropagation 과정을 통해서 가중치 행렬 $W_{a}$를 학습하게 된다.
Attention의 장점 및 특성
- Seq2Seq 모델에 Attention 모듈이 추가되면서 기계번역 분야에서 성능을 굉장히 많이 향상시켰다.
- Decoder의 매 timestep 마다 입력 sequence에서의 어떤 부분에 정보를 집중하고 사용해서 예측에 활용
- 기존의 Seq2Seq 모델은 information bottleneck이라고 볼 수 있는 Encoder의 마지막 timestep에서의 hidden state vector만을 사용해서 번역을 수행했어야했기때문에 발생했던 긴 문장에 대해서는 번역이 잘 되지 못하는 문제를 해결하였다.

- 학습에 관점에서 gradient vanishing 문제를 해결하였다.
- Attention이 없다면 위 빨간색 화살표처럼 많은 timestep을 거쳐가야 하는 long-term dependencies 문제가 있었는데 attention을 사용하게 되면서 정보의 지름길으로 볼 수 있는 파랑색 path를 이용할 수 있다.
- 어떤 timestep도 거치지 않고 attention을 계산하는 모듈을 바로 통과해서 원하는 Encoder 특정 timestep 에 hidden state vector까지 gradient를 빠르고 큰 변질없이 전달해 줄 수 있다.
- Attention 은 흥미로운 해석 가능성을 제공한다.
- Attention의 패턴이 어떤식으로 나왔는지를 조사함으로써 Decoder가 각 timestep 의 단어를 예측할 때 Encoder 상의 어떤 단어에 집중했는지를 알 수 있다.
- Decoder에서 해당하는 예측 단어에 대한 ground-truth를 통해 적용되는 softmax loss만으로 내부적인 attention module도 적절하게 학습이 되기때문에 언제 어떤 단어를 봐야하는지를 스스로 학습하는 현상을 보여준다. (end-to-end learning)
'부스트캠프 AI Tech 4기' 카테고리의 다른 글
| [NLP] 7. Transformer - Scaled Dot-Product Attention (0) | 2022.10.18 |
|---|---|
| [NLP] 6. Beam Serach and BLEU score (0) | 2022.10.17 |
| [WEEK04 마스터클래스] : 안수빈 마스터 (0) | 2022.10.13 |
| [WEEK04] 회고 (0) | 2022.10.13 |
| [NLP] 4. LSTM / GRU (0) | 2022.10.12 |