Manifold Hypothesis

 

MNIST 데이터는 28*28=784차원의 벡터로 나타낼 수 있다.

샘플들이 sparse하게 분포되어 있을 것이다.

(흰 부분보다 검은 부분에 밀집되어 있을 것)

 

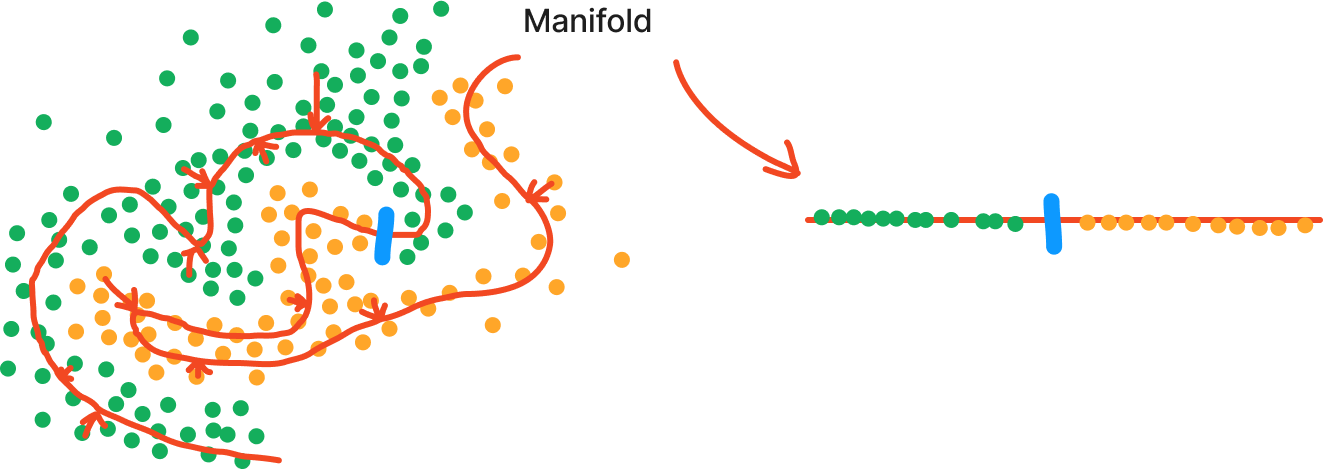
이러한 아이디어로 부터 나온 것이 Manifold Hypothesis이다.

 

 

 

 

Manifold Hypothesis

고차원 공간의 샘플들이 저차원 manifold의 형태로 분포해 있다는 가정

→ manifold를 해당 차원의 공간에 mapping할 수 있다.

https://kh-kim.gitbook.io/natural-language-processing-with-pytorch/00-cover-5/02-dimension-reduction

 

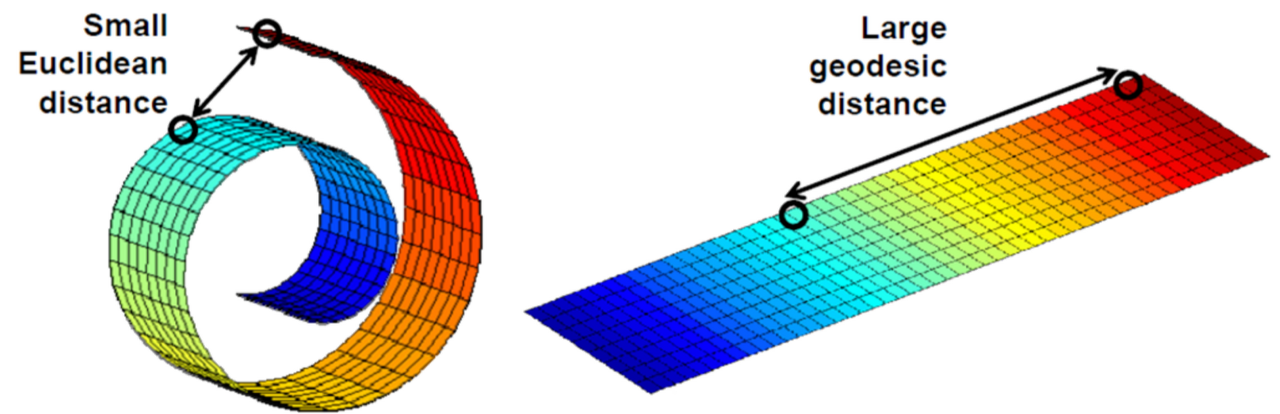
고차원의 데이터를 잘 표현하는 manifold를 통해 샘플 데이터의 특징을 파악할 수 있다.

 

 

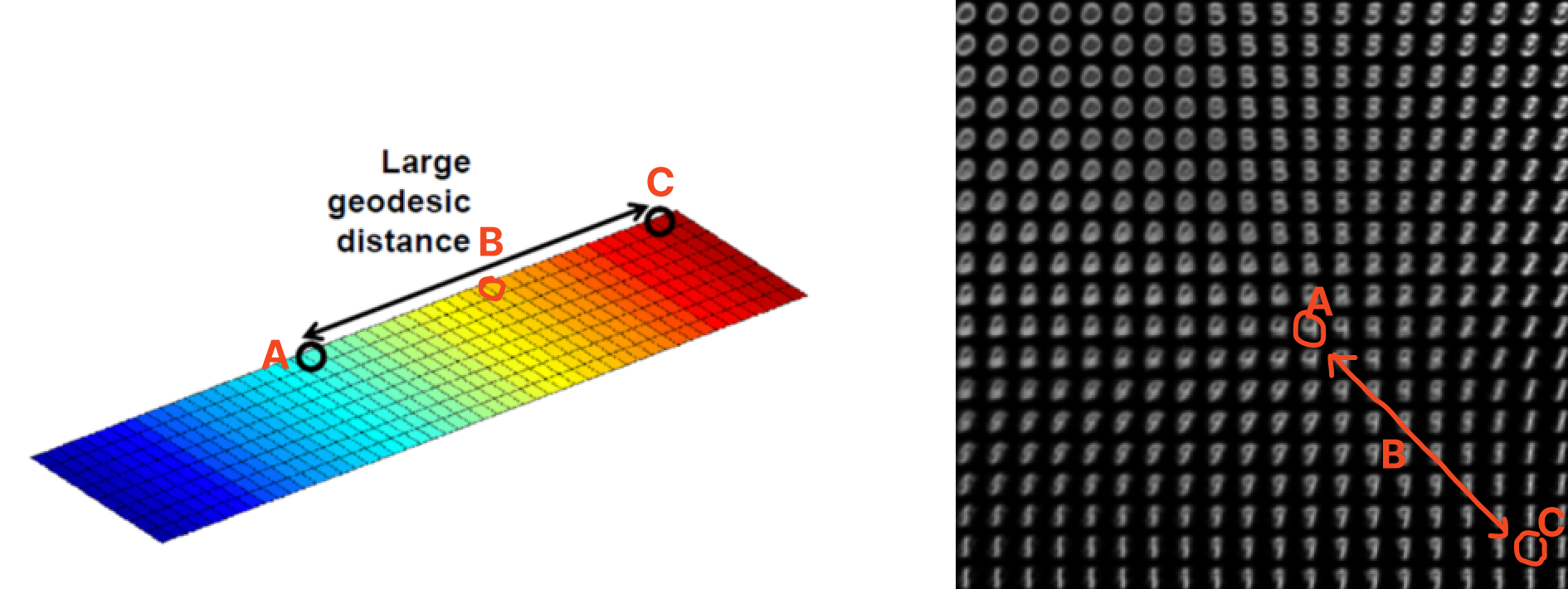
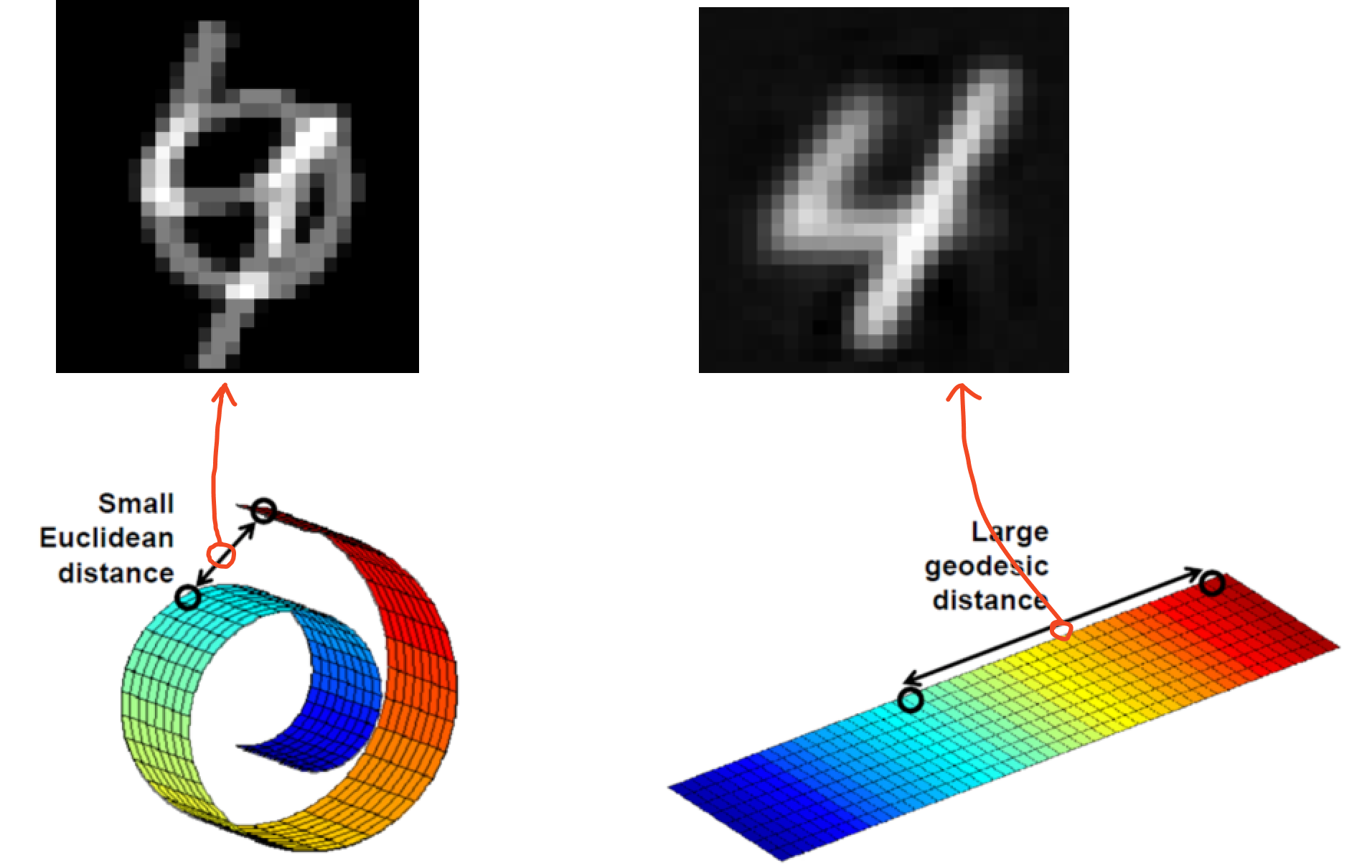
Dimensionality Reduction에는 linear한 방법(PCA, LDA...)와 Non-linear(AutoEncoder, t-sne...)가 존재하는데,

딥러닝은 Non-linear Dimension Reduction으로 아래 그림과 같이 차원 축소가 가능하다.

 

 

---

우리가 머신러닝 모델을 만드는 목적은 여태까지 있었던 데이터를 가지고 Ground truth 확률 분포 함수에 근사한 확률 분포 함수를 만드는 것이다.
근사한 확률 분포 함수를 만들 수록 미래에 들어올 데이터에 대한 태스크를 정확히 수행할 수 있을 것이다.

 

 

1. Ground truth 확률분포함수에 근사한 확률분포함수의 파라미터 θ를 찾는다.

• MLE(Maximize Likelihood Estimation):  데이터를 잘 설명하는 확률분포를 찾는 과정으로 NLL(Negative Log Likelihood)를 minimize하는 것인데 이는 Cross Entropy로 최적화를 하는 과정과 같다.
• 정보이론 관점에서 본다면 Cross Entropy를 minimize하는 것은 ground truth 확률 분포와 비슷하게(Similarity) 만드는 과정이다.
• minimize하기 위해서 Gradient descent를 수행한다.
  Gradient descent를 수행하기 위해서는 파라미터 θ를 가지고 미분해야하므로 back propagation을 수행하게 된다.

 

2. 데이터는 저차원의 manifold에 분포하고 있다.
    따라서 manifold를 잘 찾는다면 더 낮은 차원으로 효율적인 맵핑(projection)이 가능하다.
    또한 낮은 차원으로의 표현으로 차원의 저주 문제점을 해결할 수 있다.