ReLU로 어떻게 곡선 함수를 근사하나요? ❓

모델을 크게 바라보면 우리가 목적하는 task의 groundtruth에 근사(Approximation)하는 함수이다. 

딥러닝에서는 Universal Approximation Theorem이란 1개의 히든 레이어를 가진 Neural Network를 이용해 어떠한 함수든 근사시킬 수 있다는 이론으로 Approximation 함수 존재를 보장한다.

 

https://towardsdatascience.com/if-rectified-linear-units-are-linear-how-do-they-add-nonlinearity-40247d3e4792

 

ReLU 함수는 이전 레이어의 편향 및 가중치를 통해 임의의 위치에서 임의의 각도로 선형 함수를 구부릴 수 있다.

 

또한 ReLU를 여러 개 결합하면, 곡선 함수에 근사할 수 있다.

 

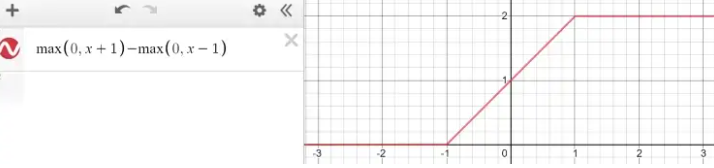
+ ReLU가 비선형 함수인 이유

선형함수일려면 동차성과 가산성이 성립해야 한다.

 

$$ ReLU = max(0, x) $$

 

1. 동차성 : $ f(ax) = a f(x) $

$ a = 2 $일 때,

$ f(2x) = max(0, 2x) $

    $ x > 0 → 2x $

    $ x < 0 → 0 $

$ 2 f(x) = 2 max(0, x) $ 

    $ x > 0 → 2x $

    $ x < 0 → 0 $

⇒ 동차성이 성립

 

2. 가산성 : $ f(x1+x2) = f(x1) + f(x2) $

$ x1 = -1, x2 = 2 $ 일 때,

$ f(-1 + 2) = f(1) = 1 $

$ f(-1) + f(2) = 0 + 2 = 2 $

⇒ 가산성이 성립하지 않음

 

 

---

https://towardsdatascience.com/if-rectified-linear-units-are-linear-how-do-they-add-nonlinearity-40247d3e4792

https://towardsdatascience.com/how-do-relu-neural-networks-approximate-any-continuous-function-f59ca3cf2c39