[DL Basic] 2. Optimization
- -
▮ Concepts in Optimization
Generalization
모델의 일반화 성능을 높이는 것이 목적이다.
Generalization은 train error와 test error간의 차이를 말한다.
train error가 0이라고 해서 test error는 성능이 오히려 떨어지게 되는 경우가 있다.
Underfitting vs Overfitting

Cross-validation
k-1개로 학습을 시키고 한 개로 validation을 하는 방법

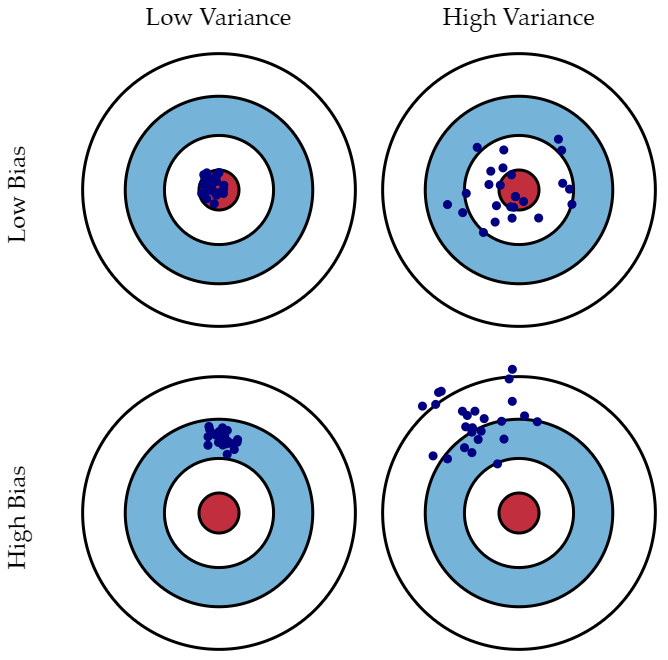
Bias and Variance
Variance : 비슷한 입력을 넣었을 때 출력이 얼마나 일관적인지
Bias : 평균적으로 봤을 때 target과 얼마나 벗어났는지
Bootstrapping
학습데이터를 sub-sampling해서 여러 개의 모델을 만드는 방법
Bagging vs Boosting
- Bagging (Bootstrapping aggregating)
여러개의 모델을 고정된 학습 데이터셋의 random sub-sampling을 통해 만들고 이 모델들의 output의 평균을 내는 방법 - Boosting
간단한 모델을 가지고 학습 데이터에 대해 돌려보는데 잘못 예측한 것에 대해서만 잘 동작하는 또다른 모델을 만들고..
여러개의 모델(weak learner)들을 sequential하게 합쳐서 하나의 strong learner를 만든다.

▮ Gradient Descent
찾고자하는 파라미터에 대해서 loss function를 편미분한 값을 가지고 loss function을 최소화시키는 파라미터 값을 찾는 방법
- Stochastic gradient descent
- single sample로부터 gradient를 계산, 업데이트하는 방식
- Mini-batch gradient descent : 대부분의 딥러닝에 활용되는 방식
- data의 subset로부터 gradient를 계산, 업데이트하는 방식
- Batch gradient descent
- 전체 data로 부터 gradient를 계산, 업데이트하는 방식
Batch 기반 최적화를 할때, Batch-size matters를 고려해야 한다.
Gradient Descent Methods (다양한 최적화 기법)
- (Stochastic) Gradient descent
$$ W_{t+1} \leftarrow W_{t} - \eta g_{t} $$
lr를 적절히 잡아주는게 중요하다.
- Momentum
$$ a_{t+1} \leftarrow \beta a_{t} + g_{t} $$
$$ W_{t+1} \leftarrow W_{t} - \eta a_{t+1} $$
$\beta$ 는 momentum으로, $a_{t+1}$는 accumulated gradient이다.
한번 gradient가 이쪽 방향으로 흐르면 다음번 gradient가 다른 방향으로 흘러도 아까 그 방향을 어느정도 활용할 수 있는 방법이다.

- Nesterov Accelerate Gradient
$$ a_{t+1} \leftarrow \beta a_{t} + \nabla L(W_{t} - \eta \beta a_{t}) $$
$$ W_{t+1} \leftarrow W_{t} - \eta a_{t+1} $$
$a$라고 불리는 accumulated gradient가 gradient descent를 하는데, gradient를 계산할 때 Lookahead gradient를 계산한다.
모멘텀은 현재 주어져있는 파라미터에서 gradient를 계산해서 그 gradient를 가지고 momentum을 accumulation을 하는 반면, NAG는 a라고 불리우는 현재 정보로 한번 이동해보고 이동한 곳에서 gradient를 계산한 것을 가지고 accumulation을 하는 것이다.
$\nabla L(W_{t} - \eta \beta a_{t})$는 Lookahead gradient이다.
Momentum보다 수렴 속도가 더 빠르다.

- Adagrad
$$ W_{t+1} \leftarrow W_{t} - \frac{\eta}{ \sqrt{G_{t}+ \epsilon } } g_{t} $$
neural network의 파라미터들 중에 많이 변화된 파라미터는 더 적게 변화시키고, 적게 변화된 파라미터는 많이 변화시킨다.
$G_{t}$는 Sum of gradinet squares로 gradient가 변화한 양을 제곱해서 더한 것이다.
이 $G_{t}$가 무한대로 가게 되면 W의 update가 안되는 문제점이 있다.
- Adadelta
$$ G_{t} = \gamma G_{t-1} + (1-\gamma)g_{t}^{2} $$
$$ W_{t+1} \leftarrow W_{t} - \frac{\sqrt{H_{t+1} + \epsilon} }{ \sqrt{G_{t}+ \epsilon } } g_{t} $$
$$ H_{t} = \gamma H_{t-1} + (1-\gamma)( \Delta W_{t})^{2} $$
$G_{t}$ : EMA of gradient squares
$H_{t}$: EMA of difference squares
앞서 한 Adagrad의 문제점을 해결하고자 한 방법이다.
현재 timestep t가 주어졌을 때 window size만큼의 파라미터에 대한 gradient 변화의 제곱을 보는 방법이다.
그러나 이 방법도 문제가 있는데, window size만큼의 G 정보를 들고 있어야한다. 1000억개의 파라미터를 갖고 있는 모델이라면 G도 1000억개의 파라미터를 들고있어 공간적으로 비효율적이다.
이러한 비효율성을 방지하기 위해 exponential moving average(EMA) 를 사용한다. ( $\gamma$와 1− $\gamma$를 곱해주는 부분)
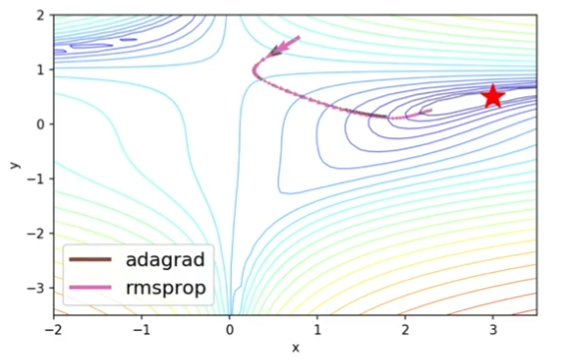
Adadelta는 learning rate가 따로 존재하지 않아서 바꿀 수 있는 부분이 많이 없어서 잘 활용되지 않는편이다. - RMSprop
$$ G_{t} = \gamma G_{t-1} + (1-\gamma)g_{t}^{2} $$
$$ W_{t+1} \leftarrow W_{t} - \frac{ \eta }{ \sqrt{G_{t}+ \epsilon } } g_{t} $$
$G_{t}$ : EMA of gradient squares
Adadelta와 마찬가지로 gradient squares의 지수이동평균을 사용하지만,
여기서는 학습률인 $\eta$를 도입해서 이를 $G_{t}$의 square root로 나눠주는 방식을 취했다.
즉, Adadelta에서 다시 학습률을 도입한 최적화 방법론이다.
- Adam
Adam 알고리즘은 adaptive learning rate 방법과 momentum을 효과적으로 합친 방법이다.
$$m_{t} = \beta_{1}m_{t-1} + (1-\beta_{1})g_{t}$$
$$v_{t} = \beta_{2}v_{t-1} + (1-\beta_{2})g_{t}^{2}$$
$$ W_{t+1} \leftarrow W_{t} - \frac{ \eta }{ \sqrt{v_{t}+ \epsilon } } \frac{ \sqrt{1-\beta_{2}^{t}} }{1-\beta_{1}^{t}} m_{t} $$
$m_{t}$ : gradient
$v_{t}$ : EMA of gradient squares
$\epsilon$ : zero division error를 방지하기 위한 항 (practice에선 꽤 중요함. 대략적으로 e-7로 조절)
▮ Regularization
학습 데이터에만 잘 동작하는게 아니라 테스트 데이터에서도 잘 동작하도록 Generalization을 잘 되게 하고 싶어서 규제를 거는 방법이다.
- Early Stopping
training에 활용되지 않은 데이터셋에 학습된 모델 성능을 평가해보고 loss가 어느시점부터 커지기 시작하면 멈추는 방법이다.

- Parameter norm penalty (weight decay)
파라미터가 너무 커지지 않게 하는 방법이다. - Data augmentation
데이터는 많을 수록 좋다. - Noise robustness
neural network의 weight나 입력값에 noise를 넣어주면 성능이 더 잘나온다는 실험적인 결과가 있다. - Label smoothing
데이터 2개를 뽑아서 이 2개를 섞어 준다.
decision boundary를 부드럽게 만들어주는 효과가 있다. - Dropout
일정 비율의 Neural Network의 weight를 0으로 바꾼다.
각각의 뉴런들이 robust한 feature를 잡을 수 있다고 해석한다. - Batch normalization
내가 적용하려고자 하는 layer의 statistics를 정규화 시키는 방법이다.
1000개의 파라미터의 각각의 값들에 대한 statistic을 평균을 빼주고 표준편차를 나눠주는 방법으로 정규화시킨다.
일반적으로 사용하면 성능이 많이 오른다.
부스트캠프 AI Tech 교육 자료를 참고하였습니다.
https://www.youtube.com/watch?v=DDZQYj4AXCA
'부스트캠프 AI Tech 4기' 카테고리의 다른 글
| [DL Basic] 4. Recurrent Neural Networks (0) | 2022.10.06 |
|---|---|
| [DL Basic] 3. CNN (1) | 2022.10.05 |
| [DL Basic] 1. Neural Networks & Multi-Layer Perceptron (0) | 2022.10.03 |
| [WEEK02 마스터클래스] 최성철 마스터 (0) | 2022.09.30 |
| [WEEK02 두런두런] 변성윤 마스터 (0) | 2022.09.29 |